Total Survey Error is one of the most popular theoretical framework in survey methodology. It supports a holistic view of the data collection process in which we should concurrently analyse different dimensions that impact data quality.
While, in principle, most researchers agree that such a framework is useful and the idea of estimating multiple types of error concurrently is beneficial, doing so in practice has proved to be challenging. Most of the methods developed to estimate data quality tend to look at one type of error at the time. This is true both for selection, e.g. regression models explaining unit non-response, and measurement, e.g. a test-retest experiment that estimates reliability.
Estimating multiple types of errors at the same time has at two important advantages. Firstly, ignoring other types of errors might bias current results. For example, the MultiTrait MultiMethod (MTMM) model assumes that no other types of measurement error are present in the data (except method effects and random error). This is can be a problematic assumption given the large literature discussing other types of measurement error, like social desirability, acquiescence, primacy/recency. If any other types of measurement error are present in the data, the estimates from the MTMM might be biased. Secondly, looking concurrently at errors makes it possible to understand their relative sizes. This is essential for prioritizing resources and future research. For example, if we find social desirability to be the largest source of error in questions measuring attitudes towards immigration we know that future designs should prioritize minimizing this above all else.
In recent work done with Daniel Oberski we have argued that it is possible to estimate concurrently multiple types of measurement errors if we bring together experimental designs and latent variables models. In a recently published book chapter we discuss in more detail how experiments can be developed to evaluate different types of measurement errors. This implies the development of explicit hypotheses regarding measurement errors and appropriate experiments to test them. Once these are implemented measurement error can be estimated using a framework like Structural Equation Modelling (SEM). We call this approach the MultiTrait MultiError (MTME) method.
Next, I will present an example of such a design and highlight the kinds of insights are possible when using the MTME approach.
An example of a MTME design
For our initial work we investigated six common questions used to measure attitudes towards immigration. We chose these as we know that attitudes can be hard to measure and the topic can be sensitive.
The UK should allow more people of the same race or ethnic group as most British people to come and live here
UK should allow more people of a different race or ethnic group from most British people to come and live here
UK should allow more people from the poorer countries outside Europe to come and live here
It is generally good for UK’s economy that people come to live here from other countries
UK’s cultural life is generally enriched by people coming to live here from other countries
UK is made a better place to live by people coming to live here from other countries
We hypotheses the presence of three types of correlated/systematic errors:
- Social desirability: the tendency to choose categories in line with perceived social norms
- Method effects: the impact of the response scale on the answer
- Acquiescence: tendency to agree with the statement regardless of the content
For each of these types of errors we need to develop a small experiment in order to see its potential impact. The quality of the results will depend on the quality of the experiments implemented. Here is how we went about it:
- Social desirability: we had statements be either positively worded or negatively worded. This is based on the idea that the question statement implies what is the social norm.
- Method effects: we had either a 11 point response scale or a 2 point one.
- Acquiescence: the response scale was either Agree-Disagree or Disagree-Agree. Previous research has shown that when the agree category is presented first respondents are more likely to select it.
Additionally, the MTME is also able to estimate random error due to the use of a within experimental design.
By combining these experiments we end up with eight different ways in which we could ask the six questions:
| Wording number | Social desirability | Number of scale points | Agree or Disagree | Item formulation (using trait 1 as an example) | |||
| W1 | Higher | 2 | AD | The UK should allow fewer people of the same race or ethnic group as most British people to come and live here | |||
| W2 | Lower | 2 | AD | The UK should allow more people of the same race or ethnic group as most British people to come and live here | |||
| W3 | Higher | 11 | AD | The UK should allow fewer people of the same race or ethnic group as most British people to come and live here | |||
| W4 | Lower | 11 | AD | The UK should allow more people of the same race or ethnic group as most British people to come and live here | |||
| W5 | Higher | 2 | DA | The UK should allow more people of the same race or ethnic group as most British people to come and live here | |||
| W6 | Lower | 2 | DA | The UK should allow fewer people of the same race or ethnic group as most British people to come and live here | |||
| W7 | Higher | 11 | DA | The UK should allow more people of the same race or ethnic group as most British people to come and live here | |||
| W8 | Lower | 11 | DA | The UK should allow fewer people of the same race or ethnic group as most British people to come and live here | |||
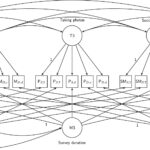
The MTME approach is a within experimental design and in order to estimate the model we need at least two measurement using two random wordings for each respondent. To collect the data we created 56 experimental groups each one receiving a combination of the eight wordings, once at the start of a survey and once at the end. We implemented the design in three waves of the Understanding Society Innovation Panel. On average there were around 30 minutes between the administration of the two types of wordings for each individual.
The MTME model
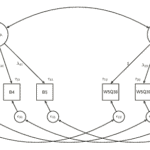
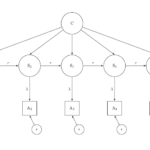
Once we design the experiment and collect the data, we need to also analyse it. To do this we used the SEM framework. We have 48 observed questions (6 questions x 8 wordings). We need to estimate 9 latent variables: 6 trait variables and 3 correlated errors.
Because we have an experimental design we can simplify the model considerably by restricting all the loadings. For the traits we can fix to 1 all the loadings to the observed items measuring the trait of interest and to 0 for the rest. For the three systematic errors there are two different approaches to defining them. We can use the dummy coding approach, where we estimate the amount of variation in one design compared to the other. This is the approach we used for the method effect (see Figure). The second approach is the effect coding approach. Here we code the loadings with -1 and +1 depending on the experimental design. This is the approach we used for the social desirability and acquiescence scales.
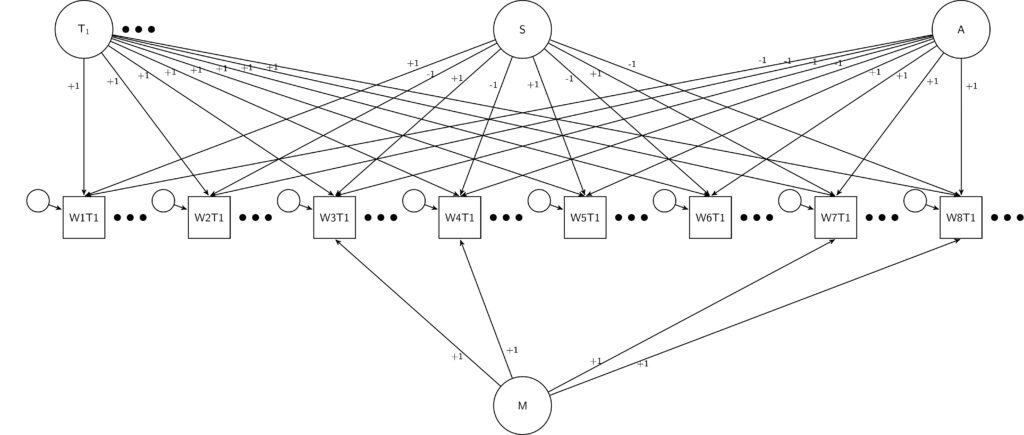
The random error is estimated using the residuals for the observed variables.
The MTME results
Based on this design and model we can concurrently investigate the effects of four types of measurement error: social desirability, acquiescence, method effect and random error. We are able to estimate the relative sizes of these effects for each question and wording. An example of how to look at the results is:
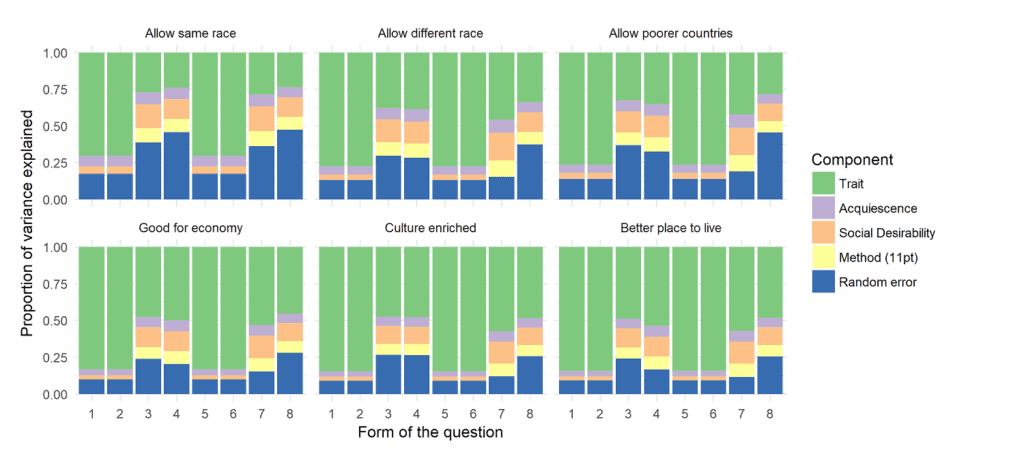
Here we see that the quality (or trait variance) varies significantly by the question and the wording/form of the question. We observe that, for example, 11 point scales tend to have lower quality compared to the 2 point scale (wordings 3, 4, 7 and 8). Similarly, we notice that the quality for the three questions is on average worse compared to the last three questions.
Conclusions
The MTME offers a flexible framework that brings together experimental designs and latent variable modelling. While the requirements are more stringent compared to other models that estimate measurement error, it offers a unique way to calculate concurrently multiple types of measurement error and get closer to the goal of a holistic approach to data quality evaluation.
You can learn more about the MTME experiments having a look at this book chapter and you can find more about the statistical modelling but looking at this peer review paper.
If you feel experimental and want to give a try to the MTME approach feel free to contact me!